Create your first model
Introduction
Setting up a mizer model that agrees with observations used to be difficult. That is not a surprise, because we have seen how all the species influence each other, as well as the resource, and how the reproduction rates of all species depend on the size spectra of all species and vice versa. So if you make changes in one corner of the model to make it agree with some observation, things change at another corner to mess things up again.
There are three dynamic processes in action in a mizer model at the same time: size-spectrum dynamics, reproduction dynamics and resource dynamics. These are fully interacting with each other, with feedback loops. So for example the resource spectrum depends on the consumption by fish, which depends on the fish size spectra, which depend on the fish growth rates, which depends on the resource spectrum. Similarly the reproduction rate depends on the number of mature fish and on their energy income, which depends among other things on the rate at which new individuals are recruited, which depends among other things on the reproduction rate. And all of these feedbacks depend on the model parameters that we are supposed to choose in a way that reproduces observed behaviour. It seems hopeless!
The way we have arrived at a simple process for the creation of a viable mizer model is to decouple the tuning of the size spectrum dynamics from the tuning of the reproduction dynamics and resource dynamics. So, as we have done last week, initially we turn off reproduction dynamics and resource dynamics. We set the constant reproduction rate to a level that produces the observed biomasses and we set the constant resource spectrum according to observations or, in the absence of observations, we set it to a Sheldon power law. We then use that size spectrum dynamics on its own. The size spectrum usually quickly settles down to its steady state, so that we can interactively tune parameters to get the steady state to agree with observations.
Once we are happy with the steady state of the model, we turn the reproduction and resource dynamics back on, but with parameter choices that do not modify the steady state of the size spectra in a now coupled system. We then have to tune the remaining parameters of the reproduction dynamics and resource dynamics to achieve the correct sensitivity of the system to perturbations away from its steady state. By separating tuning of the dynamics from the tuning of the steady state, the whole process becomes much more manageable.
We will concentrate on building models with the correct steady state this week and then tune the behaviour away from steady state next week.
In this tutorial we will take the species parameters that we assembled in the previous tutorial for the Curonian Lagoon and use the newMultispeciesParams() function to build a mizer model with them. We will let mizer choose most of the defaults and then adjust a few things so that the model has a steady state that has the observed species biomasses and growth curves. We will not do any fine-tuning of the steady state because the first big improvement that we will make in the next tutorial will be to add multiple resource spectra, as is appropriate for this shallow coastal ecosystem.
As always, we start by loading packages.
Now the creation of the mizer model is a 5-step process.
Step 1: Create MizerParams object
We have the species parameters, the gear parameters and the interaction matrix for our model saved as .csv files and we discussed these in the previous tutorial. So here we only need to read in those files.
We use rownames = 1 to let read.csv know that the first column in the spreadsheet, which contains the predator names, should be used as the names of the rows of the interaction matrix.
When you repeat this work in your worksheet, you can check that the data was read in correctly by clicking on curonian_species_params, curonian_species_params and curonian_interaction in the “Environment” tab. That will open the data frames in your editor window for you to inspect.
We will now set up a multi-species mizer model using the function newMultispeciesParams(). Besides the species parameters, the gear parameters and the interaction matrix, the other information that flows into a multi-species model are the resource parameters, the allometric exponents n and p and the fishing effort.
We let mizer choose defaults for the resource parameters. By default, the resource carrying capacity will be set to a power law N_R(w) = \kappa w^{-\lambda} with \lambda = 2.05, as we are already familiar with from week 1.
Last week we discussed that our choice for the allometric exponents n (growth exponent) and p (metabolic exponent) is to take them both equal to 3/4. By default these exponents in multi-species models are set to different values, so we will overwrite the defaults in our newMultispeciesParams() command.
With this information we call the function newMultispeciesParams() which returns a MizerParams object that we save in the variable cur_model (lazy shorthand for “Curonian model”):
cur_model <- newMultispeciesParams(species_params = curonian_species_params,
gear_params = curonian_gear_params,
interaction = curonian_interaction,
initial_effort = 0.3,
lambda = 2.05, n = 3/4, p = 3/4)No h provided for some species, so using f0 and k_vb to calculate it.
No ks column so calculating from critical feeding level.
Using z0 = z0pre * w_inf ^ z0exp for missing z0 values.As you see from the messages it has printed, the newMultispeciesParams() function has made choices for some model parameters based on the information we supplied.
So for example it chose the coefficient h of the maximum intake rate for each species to produce growth curves that are roughly in agreement with the von Bertalanffy growth parameters k_vb that we supplied and with a larval feeding level f0 (which we did not supply but which mizer chose as f0 = 0.6).
Mizer chose the coefficient ks of the metabolic rate for each species so that a proportion fc of the maximum intake rate would be enough to cover the metabolic expenses. We did not specify this critical feeding level fc so mizer chose fc = 0.2.
Finally mizer has set a constant background mortality z0 that scales with the species’ asymptotic size. Let’s look at the result:
species_params(cur_model) |> select(h, ks, z0)Step 2: Project to steady state
The newMultispeciesParams() function is not very good at choosing a good initial community configuration. Let’s have a look at what it has set up:
plotSpectra(cur_model, power = 2)
There is a lot wrong here. The species spectra lack the characteristic bulge at adult sizes. Also the species spectra do not line up nicely with the abundance of the resource. But most importantly, these spectra are not close to their steady state values.
We will now project to the steady state, which will finally give us realistic species spectra. To do this we use the special function steady() which implements our trick of keeping the reproduction rate and the resource spectrum constant.
cur_model <- steady(cur_model)Convergence was achieved in 18 years.Warning in setBevertonHolt(params, reproduction_level =
old_reproduction_level): The following species require an unrealistic
reproductive efficiency greater than 1: roachWe can ignore the warning from the setBevertonHolt() function about unrealistic reproductive efficiencies. Those warnings are an artefact of how the reproduction level is set by default by the matchBiomasses() function. We could fix those defaults, but we are not yet concerned with the reproduction dynamics so we don’t have to do that and just ignore the warnings.
Remember, the steady() function does not yet calibrate your model to any observed biomasses or catches. It simply runs the model to find a state where species spectra stop changing. If you start a simulation from initial biomasses that the set of current species and resource parameters cannot support, species biomasses will change drastically at the start. Perhaps there are too many predators at the start, or too many fish for the resource to support it. After a while these fluctuations will settle down (hopefully) and species biomasses will be stable for a given set of parameters. Of course, since we are keeping reproduction and resource levels constant, this is not yet a final model.
Now let us look at the spectra in the steady state:
plotlySpectra(cur_model, power = 2)The steady() function is not guaranteed to find the steady state. It may be that the steady state is actually unstable. In that case the system evolves towards an oscillating state instead. Luckily, this is rare for realistic parameters, but may well happen while you are still trying to find the correct parameters. Let us illustrate this in a modified model. We decrease the width of the feeding kernel for all species to sigma = 1 and increase the slope of the resource spectrum to lambda = 2.2. We know from mathematical studies that both of these changes have a destabilising effect.
modified_species_params <- curonian_species_params
modified_species_params$sigma <- 1
modified_model <-
newMultispeciesParams(species_params = modified_species_params,
interaction = curonian_interaction,
initial_effort = 0.3,
lambda = 2.2, n = 3/4, p = 3/4)No h provided for some species, so using f0 and k_vb to calculate it.
No ks column so calculating from critical feeding level.
Using z0 = z0pre * w_inf ^ z0exp for missing z0 values.Now let us see what happens when we try to run this system to steady state:
modified_model <- steady(modified_model)Simulation run did not converge after 99 years. Value returned by the distance function was: 0.759089044351551The simulation has not yet converged to a steady state after running the simulation for 99 years. There are now two possibilities: 1) we just need to be a bit more patient and run the simulations for longer or 2) the system will continue to oscillate for ever. To diagnose this, we want to see the time evolution. We tell the steady() function that we want it to return a MizerSim object with the time series of spectra from the simulation.
sim <- steady(modified_model, return_sim = TRUE)The resource carrying capacity has been commented and therefore will not be recalculated from the resource parameters.Simulation run did not converge after 99 years. Value returned by the distance function was: 1.73924911721525The resource carrying capacity has been commented and therefore will not be recalculated from the resource parameters.We can now plot the time series of the species biomasses:
plotBiomass(sim)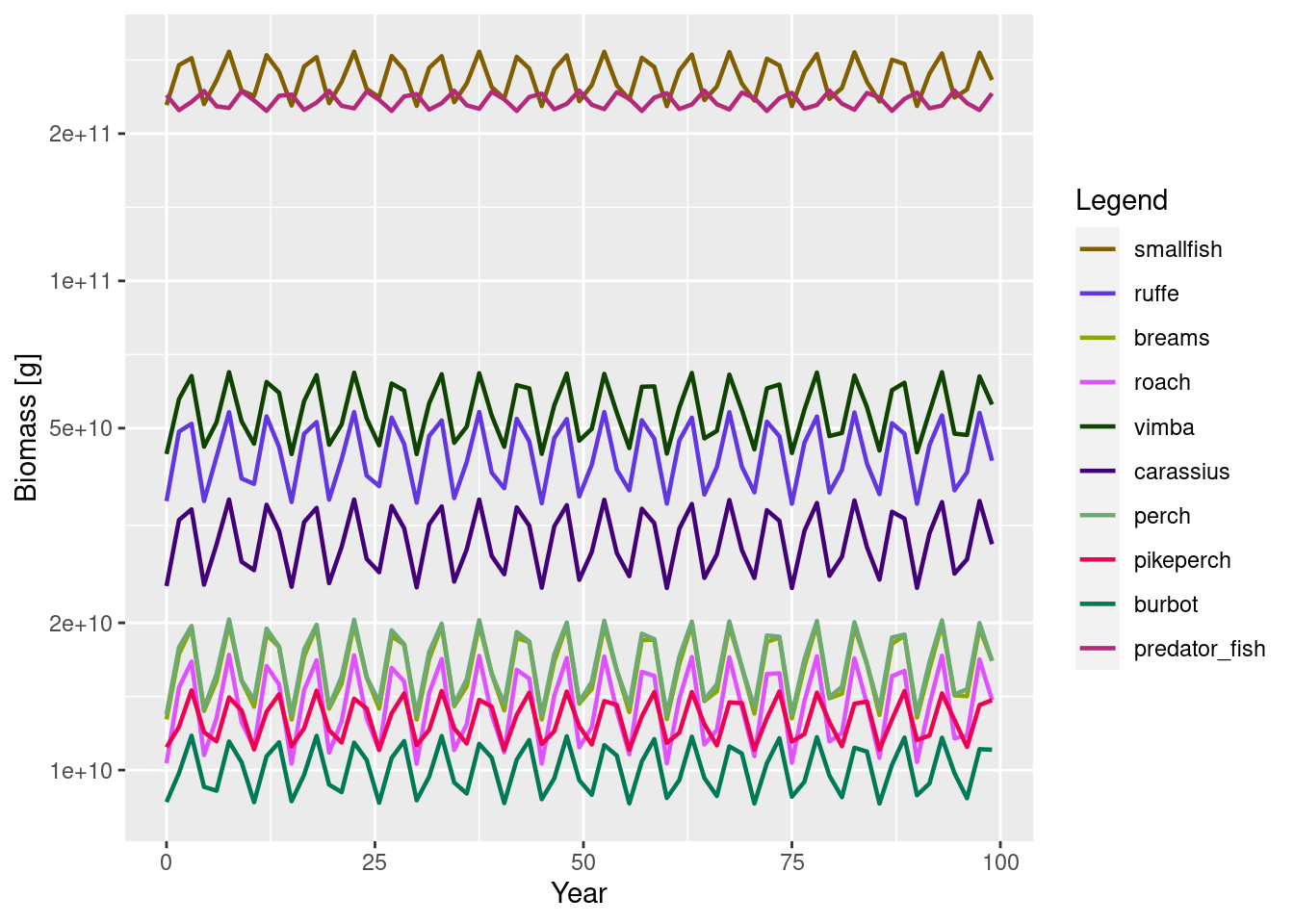
We see that the system has indeed settled into a periodic state.
We will not go into a discussion of whether the oscillating state reflects the true state of the system. We know that we can stabilise the steady state by moving the power-law exponent closer to 2 and/or by increasing the widths of the feeding kernels sigma, so unless we have good information about these parameters, it is probably easiest to just change them to stabilise the steady state, at least while tuning the model. Investigation of possible oscillatory behaviour can always happen at a later stage of model development.
Step 3: Calibrate the scale
Mizer is agnostic of whether you want to measure biomass per square meter, or per square kilometer, or for the entire area of the fishery or whatever. So initially it had set things up on an arbitrarily chosen scale. We can see this if we compare the biomasses of the species in the model with the observed biomasses from your species parameter file with the plotBiomassVsSpecies() function:
plotBiomassVsSpecies(cur_model)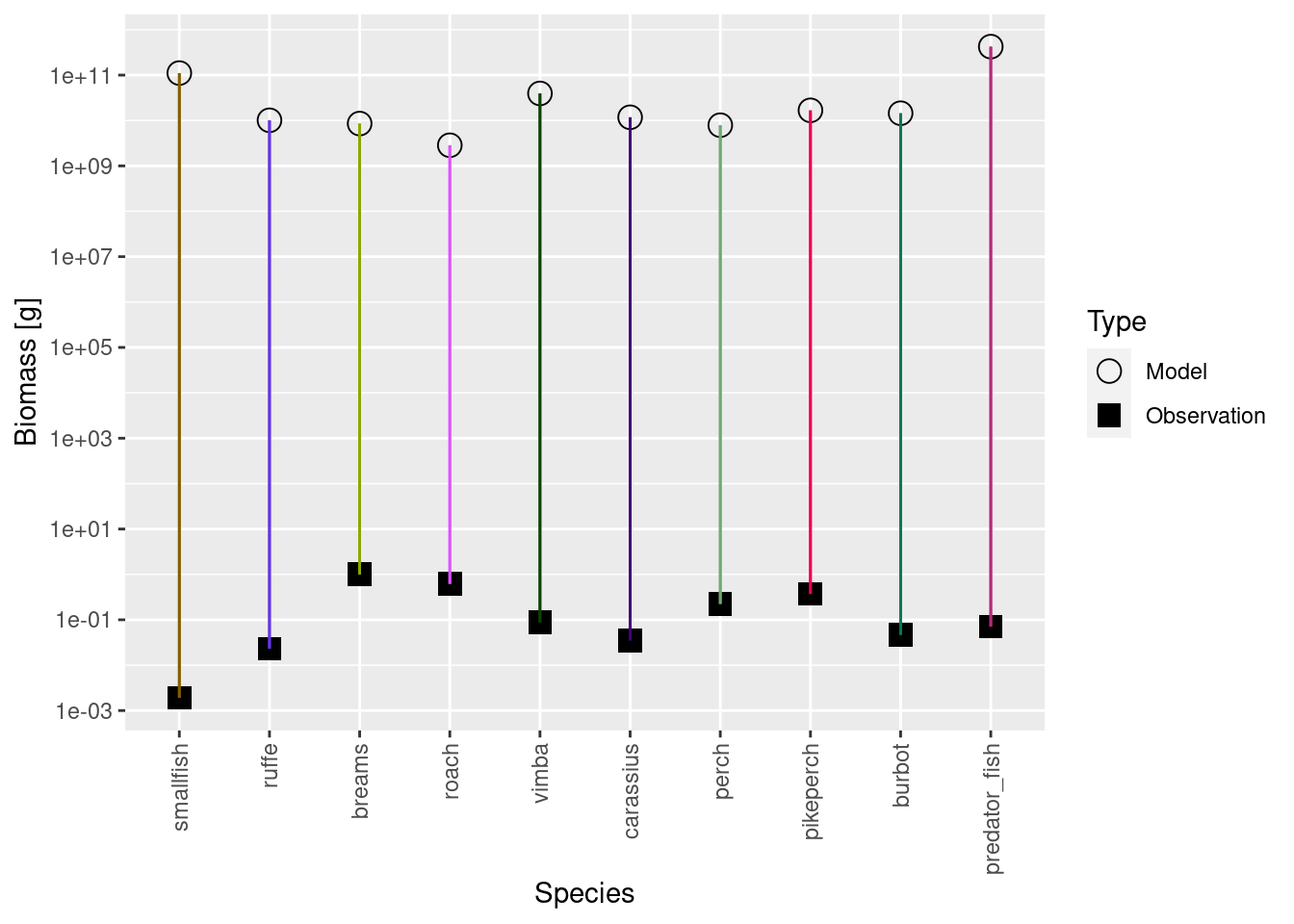
This shows for each species the model biomass (open circle) and the observed biomass (filled square) on a logarithmic y-axis. The line connecting model value and observed value is for visual purposes only. We see that model values and observed values are many orders of magnitude apart.
Using your supplied biomass observations, mizer can now change the scale of our model so that the total biomass in the model coincides with the total observed biomass, summed over all species.
cur_model <- calibrateBiomass(cur_model)Of course for the individual species the model biomasses will still disagree with the observed biomasses, with some being too high while others are too low. Just the total summed over all species agrees between model and observation.
plotBiomassVsSpecies(cur_model)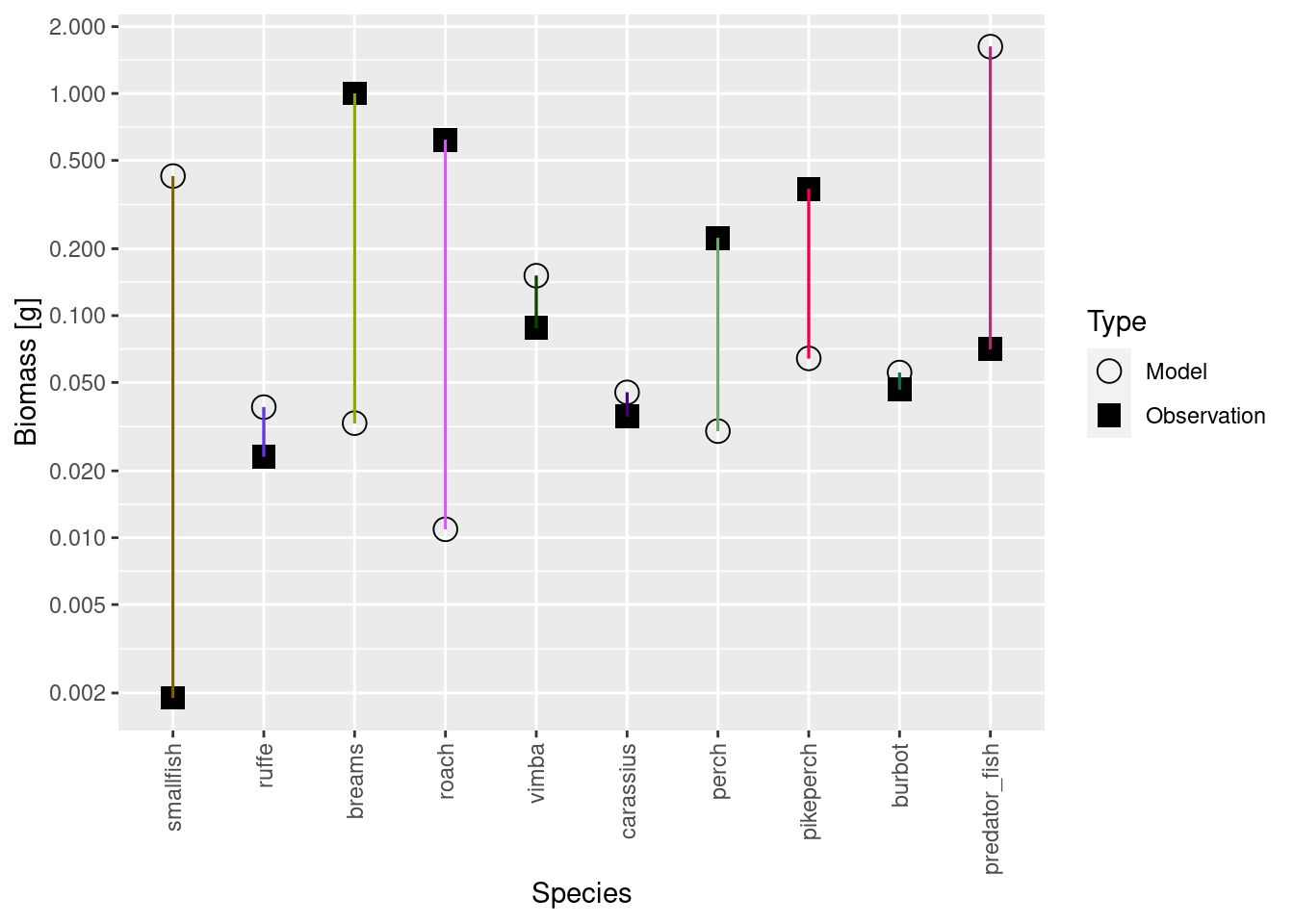
Step 4: Rescale species spectra
To fix the discrepancy between the model biomasses and the observed biomasses we simply need to rescale the model abundance of each species by the appropriate factor. The matchBiomasses() function does this for us.
cur_model <- matchBiomasses(cur_model)
plotBiomassVsSpecies(cur_model)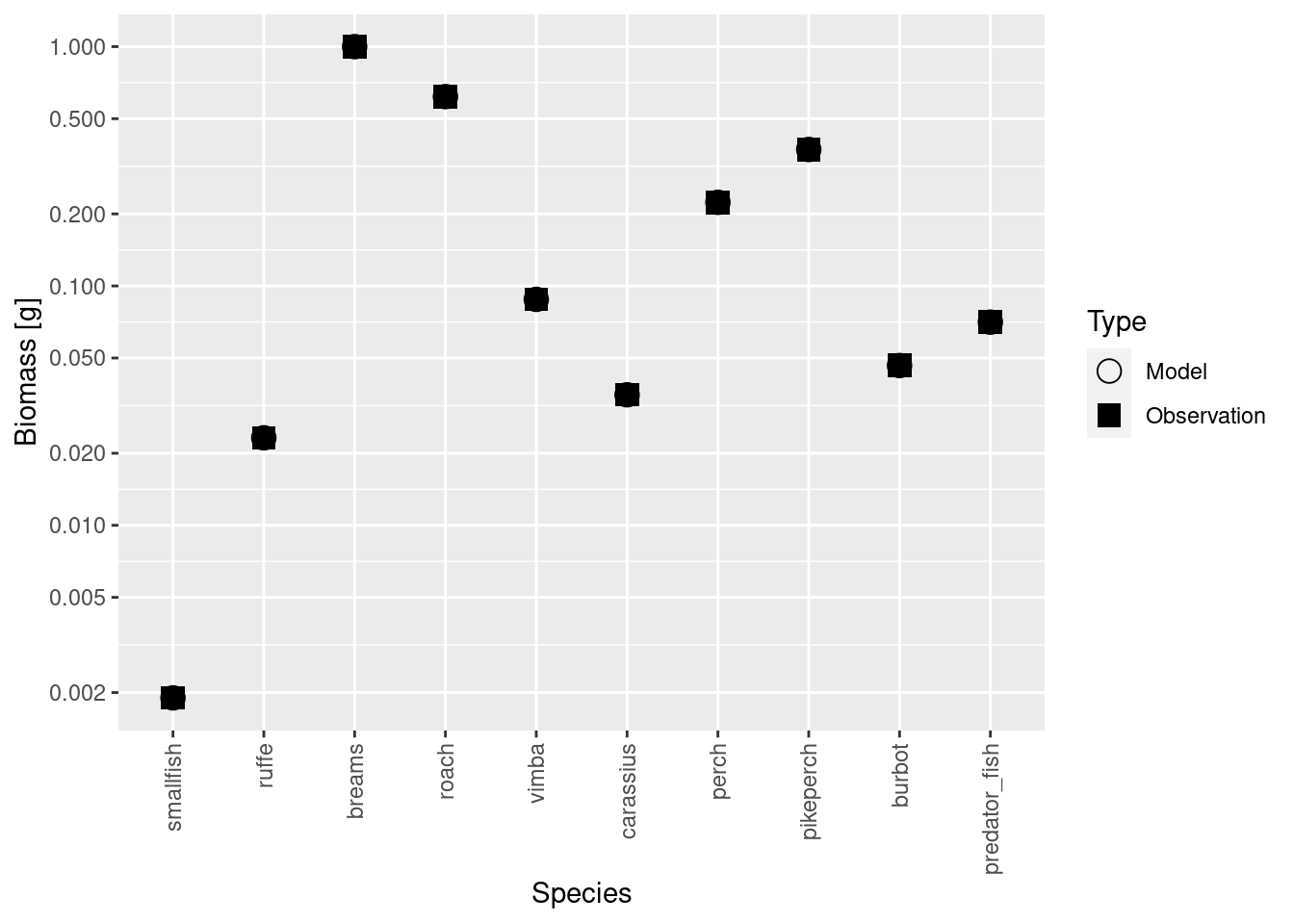
Now the circles and squares lie exactly on top of each other. This is expected, because we simply changed the relative biomasses of species in the model.
There are similar functions matchNumbers() and matchYields() that you would use in case either total numbers of individuals or fisheries yields are known instead of total biomasses.
Step 5: Rinse and repeat
After we have rescaled the spectra of the individual species, the system is no longer in a steady state. All species now experience a new prey distribution and a new predator distribution and so their growth and death rates have changed, which requires us to run the dynamics again to find the new steady state. So we essentially go back to step 2 and project to steady state:
cur_model <- steady(cur_model)The resource carrying capacity has been commented and therefore will not be recalculated from the resource parameters.Simulation run did not converge after 99 years. Value returned by the distance function was: 0.0503305492224774The resource carrying capacity has been commented and therefore will not be recalculated from the resource parameters.The function tell us that running the dynamics for 99 years was not enough to converge sufficiently close to the steady state. In other words, the state was still changing after 99 years. There are now two possibilities: 1) we simply need to be a bit more patient or 2) the dynamics will never converge to a steady state but instead continue to oscillate for ever. Let’s hope for the first option and call steady() repeatedly in the hope to eventually converge to a steady state.
cur_model <- steady(cur_model)The resource carrying capacity has been commented and therefore will not be recalculated from the resource parameters.Convergence was achieved in 63 years.The resource carrying capacity has been commented and therefore will not be recalculated from the resource parameters.We were lucky and it worked eventually.
But while the system settled down to the new steady state, the species biomasses have changed, so they now no longer agree with observation.
plotBiomassVsSpecies(cur_model)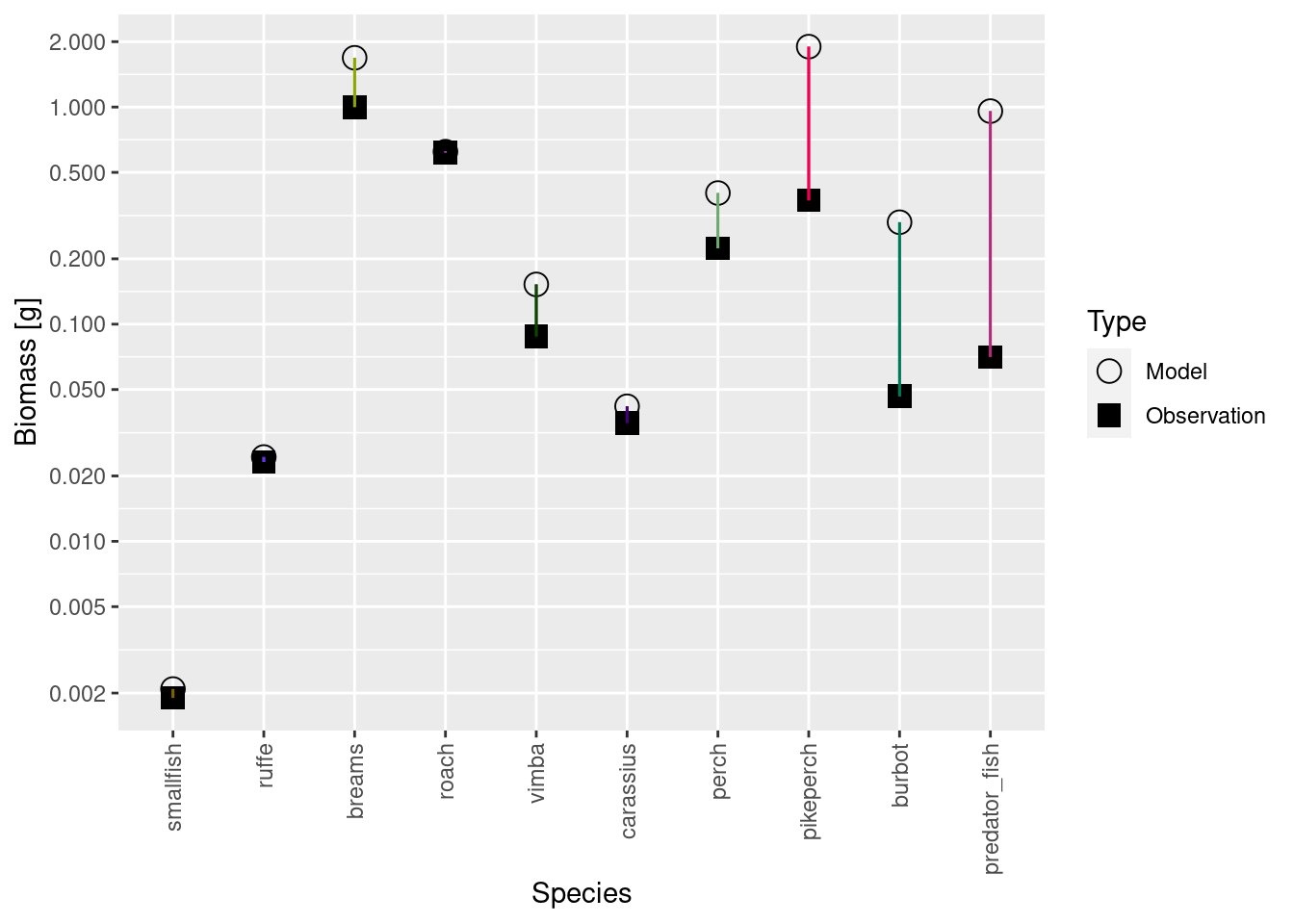
We appear to be in a bind: If we match the biomasses we are no longer at steady state, if we run to steady state we no longer match the biomasses. But notice that the discrepancies are not as big as previously. So we don’t give up but simply keep iterating, by repeatedly matching biomasses and running to steady state.
After repeating the cycle of matching biomasses and running to steady state 10 more times we get this picture:
cur_model <- cur_model |>
matchBiomasses() |> steady() |> matchBiomasses() |> steady() |>
matchBiomasses() |> steady() |> matchBiomasses() |> steady() |>
matchBiomasses() |> steady() |> matchBiomasses() |> steady() |>
matchBiomasses() |> steady() |> matchBiomasses() |> steady() |>
matchBiomasses() |> steady() |> matchBiomasses() |> steady()
plotBiomassVsSpecies(cur_model)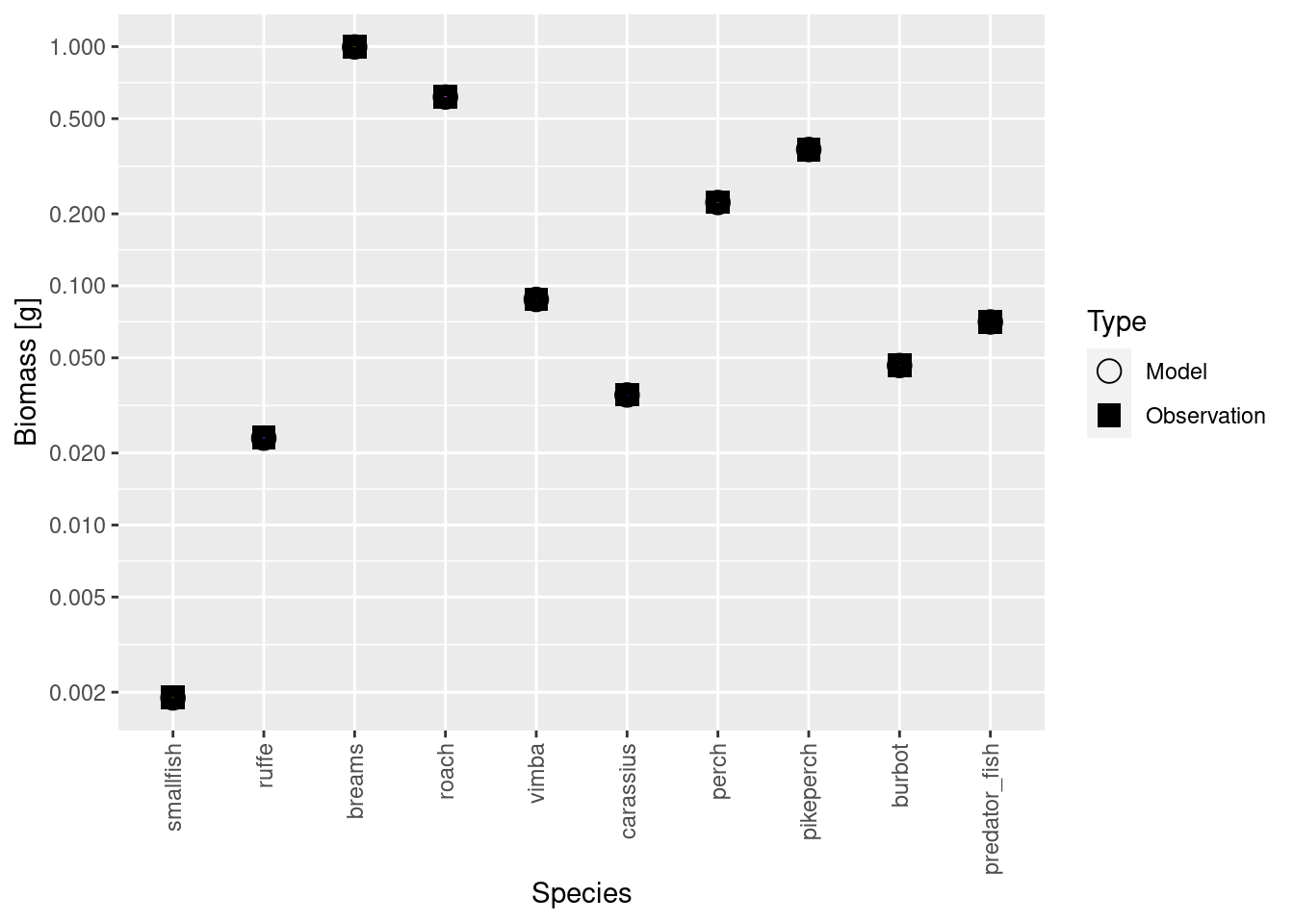
And here is how the spectra look with the correct observed biomasses:
plotSpectra(cur_model, power = 2)
Note that above we only repeated matchBiomasses() and steady(). We did not repeat calibrateBiomasses(). We could have done that, i.e., we could have run
cur_model <- cur_model |>
calibrateBiomass() |> matchBiomasses() |> steady() |>
calibrateBiomass() |> matchBiomasses() |> steady() |>
calibrateBiomass() |> matchBiomasses() |> steady() |>
calibrateBiomass() |> matchBiomasses() |> steady()This is what we proposed in this blog post. Either method works.
We can now save the resulting model to disk for future use. We choose the file name to remind us that this is the version of the model with a single resource only. We will add a benthic resource in the next tutorial.
saveParams(cur_model, "cur_model_single.rds")Exercise
Now use your species parameter data frame that you assembled in the exercise in the previous tutorial. Use the worksheet for this tutorial “worksheet-2-create-first-model.Rmd” to go through the 5 steps that we went through above to build your own mizer model based on your species parameters.
There are ways how the above method can fail. If that happens, there are various ways to rescue the situation. But rather than discussing such eventualities in the abstract, we will wait to see if you run into concrete difficulties. If you do, please save your code and email gustav.delius@gmail.com. We will then use your example to discuss the solutions.
Summary
We have gone through the 5-step process of building a mizer model from your species parameters and your interaction matrix. The 5 steps were:
Create a MizerParams object with
newMultispeciesParams().Find a coexistence steady state with
steady().Set the scale of the model to agree with the observed total biomass with
calibrateBiomass(). This does not spoil the steady state.Use
matchBiomass()to move the size spectra of the species up or down to match the observed biomasses. This will spoil the steady state.Iterate steps 2 and 4 as often as you like to get the steady-state biomasses to agree as precisely with your observations as you like.